Les chatons ont la réponse – FCSC 2020 // SMIC2

vous reprendrez bien une deuxième tournée de RSA ?

Théorie

Chers chatons, cette fois-ci nous avons l’inverse à réaliser, nous devons déchiffrer le message (c) afin de produire le message en clair (m).
À la fin de l’exercice précédent, je vous avais promis un peu plus ardu ? Nous y sommes !

Explication

Si vous vous souvenez bien, pour produire le texte (c), nous devions réaliser l’opération mathématique suivante :
c = m^e.mod(n)
Mais que disait Wikipedia pour le déchiffrement ? Qu’il tenait sur la formule suivante :
m = c^d.mod(n)

Cool, donc on a la solution ?

Non, enfin si, mais pas dès le début. Lors de SMIC1, j’avais évoqué que l’ensemble du système tenait sur la robustesse du modulus (n), ce qui n’est pas totalement exact car il faut aussi prendre en compte la robustesse de (e), mais je préfère éviter de vous perdre.
Revenons à (n), dans la génération RSA du couple de clefs, (n) repose sur le produit de deux nombres premiers entiers (p) et (q), ces nombres sont la base, et une fois que nous les avons retrouvés, nous allons pouvoir dériver la clef privée.

C’est l’heure de l’exercice de math

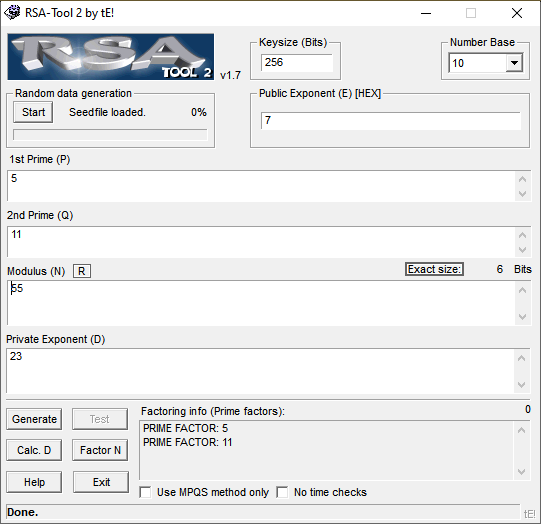
Prenons l’exemple suivant :
e = 7
p = 5
q = 11

Avec ce triptyque, nous allons pouvoir générer une pseudo paire de clefs. Commençons par la clef publique :

n = p*q = 5* 11 = 55

Nous pouvons aussi trouver Phi(n), qui sera utile pour dériver la clef privée :

Phi(n) = (p-1)*(q-1) = (5-1)*(11-1) = 4*10 = 40

et nous pouvons donc dériver notre clef privée (e^-1 se dit “inverse de (e)”):

e.d = 1.mod(Phi(n))

d = e^⁻1 .mod(Phi(n))

d = 7^-1.mod(40) = 23

RSA-Tool 2, je l’ai depuis des années, je ne remercierais jamais assez the Egoist! pour cette merveille

Retour au défi

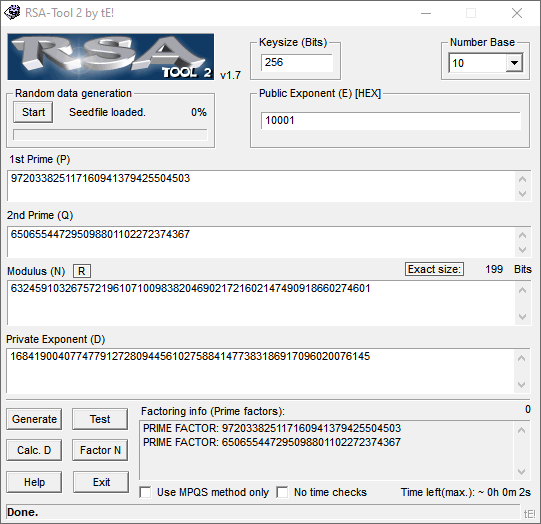
Si tu as compris où je voulais en venir, génial, sinon, il est encore temps de te raccrocher au wagon,. Nous allons factoriser (n), afin de trouver les deux nombres premiers entiers qui le composent, afin de dériver la clef privée comme au dessus. ATTENTION, nous pouvons factoriser UNIQUEMENT si le modulus (n) est considéré comme faible, ici il fait 199 Bits, ce qui est en dessous des standards et il est donc factorisable.

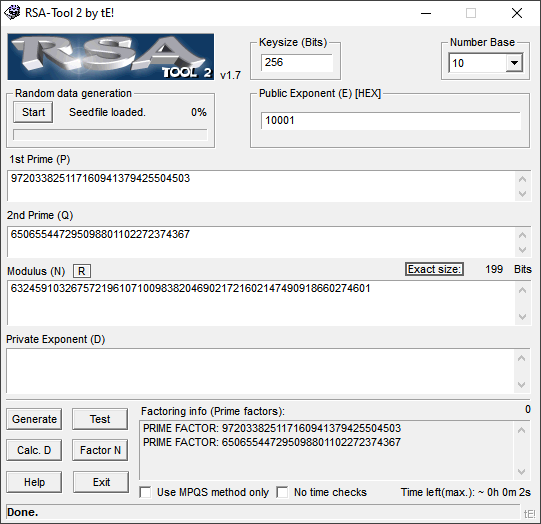
moins de deux minutes et les facteurs sont trouvés

Maintenant que nous avons les facteurs, il ne nous reste plus qu’a dériver la clef privée D, un petit clic sur le bouton et la réponse est instantanée

Exploit.py

n = 632459103267572196107100983820469021721602147490918660274601

c = 63775417045544543594281416329767355155835033510382720735973

d = 168419004077477912728094456102758841477383186917096020076145


try:
    m = pow(c,d,n)
    print("[*] Flag is : FCSC{%s}" % m)

except:
    print("[*] Sorry, better luck next time")

Voilà, un nouveau flag dans notre collection, bien joué mes chatons ! Le flag pour cet exercice était le suivant :

[*] Flag is : FCSC{563694726501963824567957403529535003815080102246078401707923}